کمانش زمانی ایجاد می شود که در اثر یک بار محوری فشاری، عضوی از سازه که تحت بار قرار گرفته به صورت ناگهانی از وضعیت صاف و مستقیم خود خارج شده و خم شود. (Collapse کند.) در واقع وقتی به یک عضو بلند، نیروی محوری فشاری وارد می شود، ممکن است در این عضو تغییر شکل جانبی ایجاد شود.

بر اساس ویژگی های عضو تحت بار، ممکن است به صورت کامل در اثر کمانش بشکند یا اینکه در ناحیه پس کمانش باقی بماند.

اما اهمیت اصلی کمانش چیست؟ پدیده کمانش می تواند در اثر نیروهایی کوچک تر از نیرویی که عضو را به شکست می رساند، ایجاد شود.

فرض کنید نیروی F می تواند تنش را از استحکام نهایی در عضو، فراتر ببرد. با وارد شدن نیرویی کمتر از F ، ممکن است عضو فوق تحت کمانش خم شود و حتی به شکست برسد. اگر سازه صرفا بر اساس استحکام نهایی طراحی شود، ممکن است تحت پدیده کمانش به شکست برسد.

بعضی از اعضا، استعداد بیشتری برای قرار گرفتن تحت کمانش دارند. مثلا تیرها، میله ها، خرپاها، پوسته ها، صفحات و …

ستون AB را در نظر بگیرد. نیروی محوری و فشاری P به آن وارد می شود. ممکن است این نیرو به حدی بزرگ نباشد که تنش ایجاد شده در ستون، از استحکام نهایی فراتر برود. اما همین نیروی P اگر به نیروی بحرانی برسد، می تواند باعث ایجاد کمانش در ستون شود. اگر در طراحی ستون به کمانش در آن توجه نداشته باشیم، طبیعتا طراحی را به درستی انجام نداده ایم.

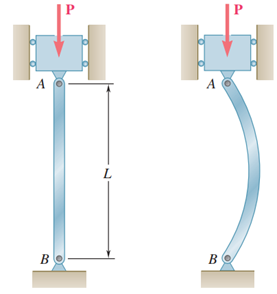
پدیده کمانش، به تعادل در سیستم مرتبط می شود. در صورتی که کمانش انجام شود، این تعادل از بین می رود.

برای اینکه بحث تعادل را بهتر درک کنیم، مدل ساده شده زیر را در نظر بگیرید. در این حالت ستونی را فرض می کنیم که از دو بخش کاملا صلب AC و BC تشکیل شده باشد. این دو بخش با یک پین به هم متصل شده اند و برای کامل تر شدن مدلسازی، یک فنر پیچشی هم در قسمت اتصال قرار گرفته است.

اگر مشابه شکل سمت چپ، دو نیرو دقیقا به صورت همراستا با میله ها وارد شوند، هر دو میله صلب به صورت عمودی باقی می مانند و می توانیم بگوییم تعادل باقی می ماند. اما چنانچه نقطه C کمی به سمت راست جابجا شود، دیگر نیروها در امتداد میله ها نخواهند بود و زاویه ایجاد شده بین دو میله افزایش می یابد. یعنی دو میله با گذشت زمان به سرعت از حالت اولیه و تعادل خود فاصله می گیرند. در این حالت دیگر تعادلی در کار نیست و سیستم ناپایدار شده است.

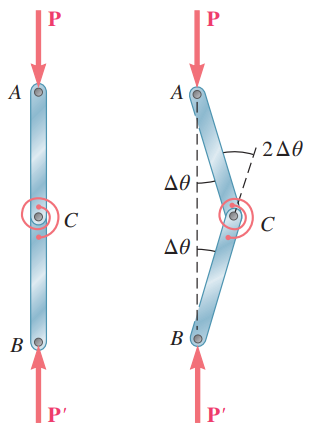
در این حالت به خاطر وجود نیروی P یک گشتاور حول نقطه C ایجاد می شود که تلاش می کند سیستم را از حالت تعادل خارج کند. از طرفی با توجه به تغییر زاویه ایجاد شده، یک گشتاور در خلاف جهت گشتاور اولیه، توسط فنر پیچشی ایجاد می شود که تلاش می کند سیستم را به حالت اولیه بازگرداند.

اگر گشتاور دوم بزرگ تر باشد، سیستم به حالت اولیه برمی گردد و در تعادل باقی می ماند. اما اگر گشتاور اول بزرگتر باشد، سیستم را از حالت تعادل اولیه خارج کرده و آن را ناپایدار می کند.

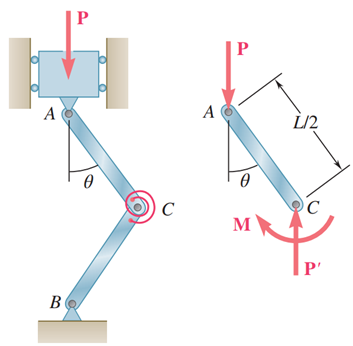
در حالتی که گشتاور های ایجاد شده توسط نیرو و توسط فنر پیچشی برابر باشد، به نیروی وارد شده، نیروی بحرانی کمانش گفته می شود. به بیان بهتر، نیروی بحرانی حداکثر نیرویی است که می تواند وارد شود بدون اینکه سیستم را ناپایدار کند. با استفاده از روابط زیر می توانیم نیروی فوق را پیدا کنیم.

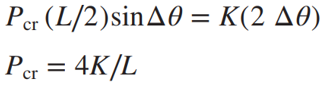
پس می توانیم بگوییم اگر نیرویی که به سیستم وارد می شود، از نیروی بحرانی که در بالا به دست آمده بیشتر بود، سیستم را ناپایدار می کند. ولی اگر نیرو کوچک تر از اندازه نیروی بحرانی به دست آمده باشد، سیستم در تعادل باقی می ماند.

می توانیم معادله بالا را به شکل زیر هم بنویسیم:

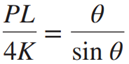
همان طور که می دانید در ناحیه مثبت، همیشه اندازه یک زاویه از سینوس آن بزرگتر است. پس در معادله بالا در حالتی که زاویه مثبت باشد، کسر سمت راست حتما بزرگ تر از 1 است. پس سمت چپ هم باید بزرگتر از 1 باشد. بزرگتر بودن کسر سمت چپ از 1، به معنی بزرگتر بودن نیروی وارد شده از نیروی بحرانی است. پس این کسر هم نتایج قبلی را تایید می کند.

فرمول اویلر برای ستون های دو سر مفصل (پین)

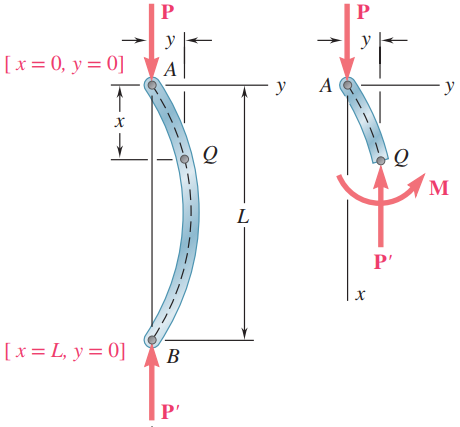
ستون را به عنوان یک تیر در نظر می گیریم که به صورت عمودی قرار گرفته و یک نیروی محوری به آن وارد می شود. با نوشتن اندازه گشتاور در هر مقطع می توانیم به رابطه زیر برسیم و معادله خطی و همگن به دست آمده را حل کنیم.

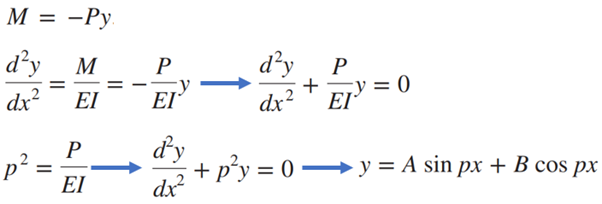
با در نظر گرفتن شرایط مرزی، می توانیم ثوابت رابطه بالا را به دست آوریم.

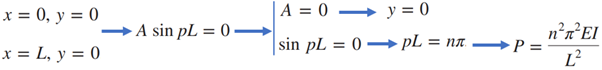
کمترین مقدار P که با استفاده از معادله بالا می توانیم به دست آوریم، به ازای n برابر با 1 است. در این حالت، نیروی بحرانی به صورت زیر محاسبه می شود:

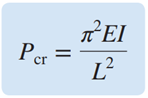
به رابطه بالا، فرمول اویلر گفته می شود.