
ماتریس سختی در المان محدود – در ادامه آموزش های مربوط به مبحث المان محدود، به بحث ماتریس سختی می رسیم. پیدا کردن ماتریس سختی، یکی از مهم ترین گام ها در المان محدود است. در این آموزش سعی کرده ایم مهم ترین نکات درباره ماتریس سختی را به زبان ساده بیان کنیم. اگر با ماتریس های سختی و نحوه به دست آوردن آنها آشنایی قبلی ندارید، ممکن است در ابتدای بحث کمی گیج شوید. اما حتما آموزش را تا انتها دنبال کنید. چون در ادامه مثالی آورده ایم که با مطالعه آن، مفاهیم به خوبی برای شما جا می افتد. ممنون از اینکه همراه ما هستید.
سایر آموزش های مربوط به المان محدود را هم می توانید در این بخش ببینید!
پله اول از آخر! اصلا چرا باید ماتریس سختی را به دست آوریم؟
بهتر است نتیجه ای را که در انتهای آموزش گرفته می شود، در همین ابتدا بیان کنیم تا در طول مطالعه با هدفمندی بیشتری آموزش را دنبال کنید. هدف از به دست آوردن ماتریس سختی چیست؟ این ماتریس چه کمکی به حل مسئله المان محدود می کند؟
برای پاسخ به این سوالات بیایید بررسی کنیم که اصلا هدف و رویکرد در حل مسئله المان محدود چیست؟ در المان محدود به دنبال این هستیم که تعدادی متغیر را به دست آوریم. یک تیر یکسر گیردار را در نظر بگیرید.
فرض کنید که کل آن را یک المان می گیریم. (این کار الزاما صحیح نیست اما اینجا برای ساده کردن مثال، این فرض را می کنیم.) حالا دو گره داریم و یک المان. مجهولات ما در این مسئله چه چیزهایی هستند؟ اولا جابجایی و شیب در گره دوم. ثانیا نیرو و گشتاور در گره اول. پس چهارتا مجهول داریم. برای بدست آوردن این مجهولات باید چهار معادله چهار مجهول تشکیل دهیم. این چهار معادله را می توانیم به صورت ماتریسی بنویسیم تا حل آن ساده تر شود. در نتیجه معادله ماتریسی زیر به دست می آید. به ماتریسی که بردار نیروها ( شامل نیرو و گشتاور) به بردار جابجایی (شامل خیز و شیب) ارتباط می دهد، ماتریس سختی است که در این آموزش قصد داریم نحوه محاسبه آن را بیان کنیم.
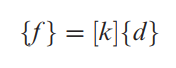
ممکن است این سوال برایتان ایجاد شود که چرا ماتریس سختی را باید محاسبه کنیم؟ چرا فقط به نوشتن ساده معادلات و حل آنها بسنده نمی کنیم؟ پاسخ این است که فرم ماتریسی، کار حل معادلات را ساده می کند. به خصوص برای نرم افزارهایی مثل آباکوس، انسیس و کامسول که بر مبنای المان محدود کار می کنند و باید همزمان معادلات را برای تعداد زیادی المان حل کنند (مثلا فرض کنید 10 میلیون!)، محاسبه مجهولات بدون فرم ماتریسی عملا غیرممکن است.
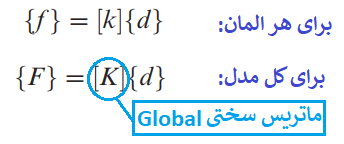
ماتریس سختی هر المان بدست می آید و سپس از اجماع این ماتریس سختی ها، ماتریس سختی گلوبال (Global) محاسبه می شود. برای به دست آوردن مجهولات از ماتریس سختی گلوبال استفاده می کنیم.
محاسبه ماتریس سختی
برویم سراغ محاسبه ماتریس سختی. ابتدا یک المان فنری را در نظر بگیرید که در ابتدا و انتهای خود گره دارد. اگر مقدار جابجایی در ابتدا و انتهای المان به اندازه u1 و u2 باشد و ضریب سختی فنر برابر k باشد، می توانیم بنویسیم:
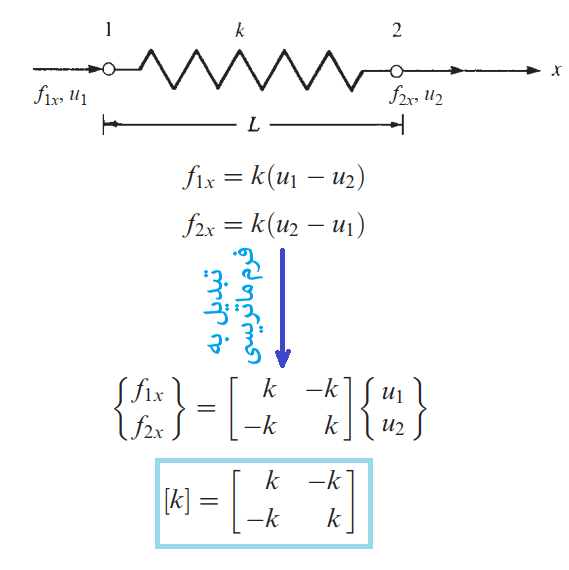
برای بدست آوردن ضریب سختی گلوبال و نیروهای گلوبال، از برهم نهی ماتریس های سختی و بردارهای نیروی تک تک المان ها استفاده می کنیم: (برای درک بهتر این موضوع، حتما مثالی را که در ادامه آموزش آمده است، با دقت بخوانید.)

اما این ماتریس برای المان های غیر فنری چگونه کاربرد دارد؟ k مربوط به آنها چگونه محاسبه می شود؟ احتمالا به یاد دارید که در مقاومت مصالح، k معادل به ازای وارد شدن نیروها و گشتاورهای مختلف را محاسبه می کردیم. مثلا به عنوان نمونه k معادل در حالت های زیر را در نظر داشته باشید.

مدل زیر را که شامل دو المان فنری است، در نظر بگیرید. در این مدل دو المان و سه گره وجود دارد. در گره های 2 و 3 ، به مدل نیرو وارد می شود. می توانیم رابطه بین نیروها و جابجایی ها را در هر المان بنویسیم.
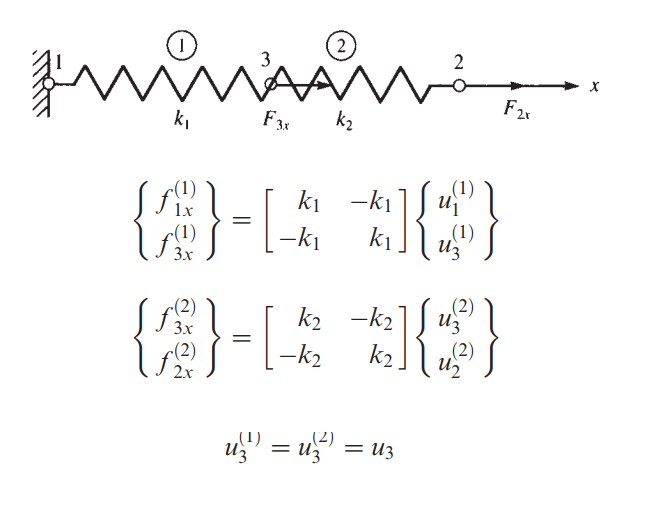
حالا با استفاده تعادل نیرویی، می توانیم روابط زیر را برای نیروهای خارجی به دست آوریم.
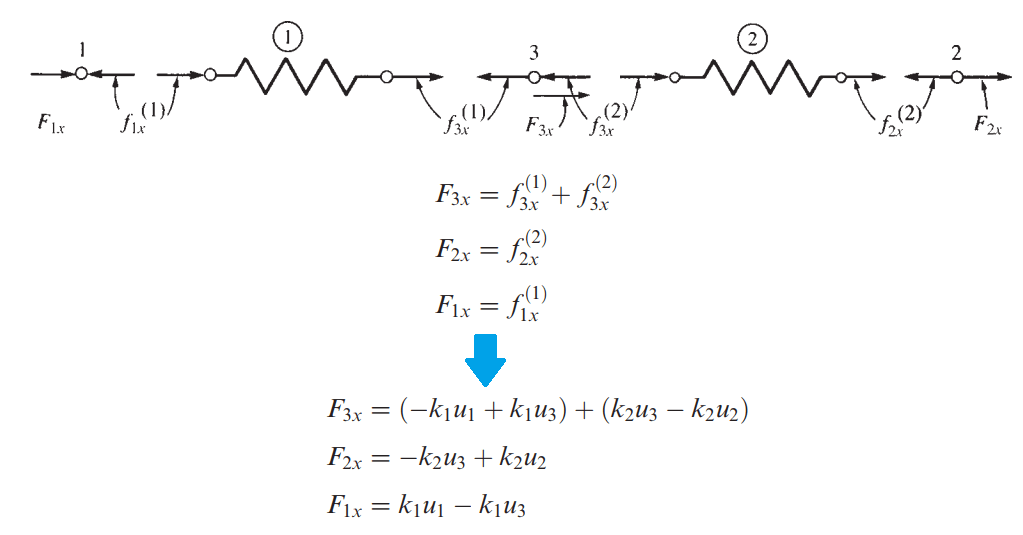
پس روابط ماتریسی به صورت زیر در می آید:
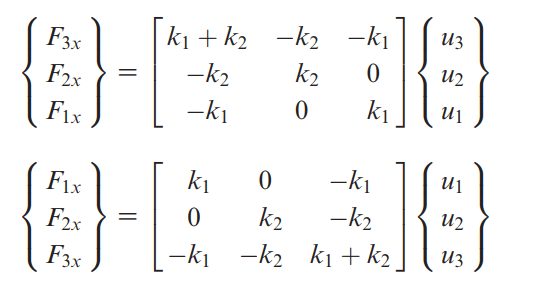
در نتیجه می توانیم ماتریس های سختی و نیروی گلوبال را به شکل زیر به دست آوریم.

اما راه ساده تر برای به دست آوردن این ماتریس ها، استفاده از اصل بر هم نهی یا سوپر پوزیشن (Superposition Principle) است. برای استفاده از این اصل، ابتدا ماتریس های سختی هر المان را به شکل زیر می نویسیم.
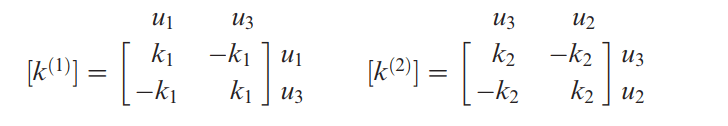
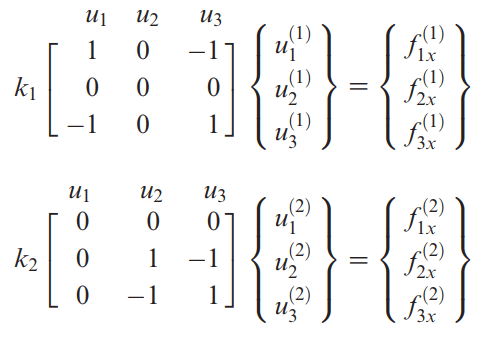
حالا طبق رابطه زیر می توانیم مقدار برایند نیروهای خارجی وارد شده به مدل را با جمع نیروهای هر گره برابر قرار دهیم.
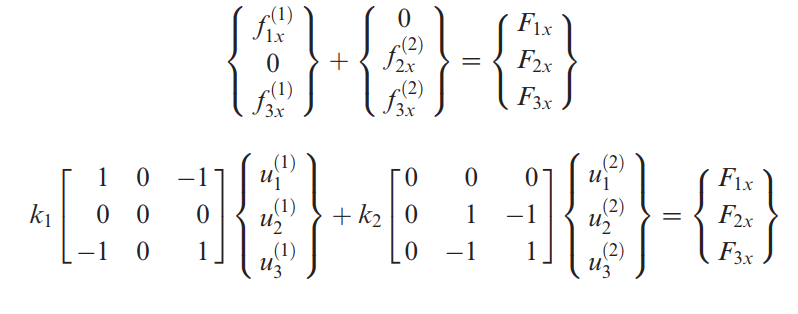
پس باز هم ماتریس سختی گلوبال، به درستی به دست می آید:
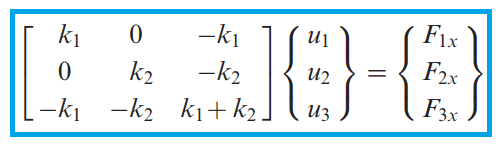
پس در این آموزش با مقدمات مربوط به ماتریس سختی آشنا شدید. به دست آوردن ماتریس سختی در مسائل مختلف با توجه به نوع مسائل، روش مشابهی دارد ولی باید قلق های خاص هر مسئله را هم بلد باشید. در آموزش های بعدی، سعی می کنیم تعدادی از این مسئله ها را هم ارائه دهیم.



ممنون برام سواال بود